Part

Part[expr,0] is always the same as Head[expr], but Head is a bit faster since
it doesn't need to determine what part.  For example Part[1+π, 0] returns
Plus.

In the next cell we see the part at position (2,0) of the list {1,1+π} is
Plus.

In the next cell a matrix (m) is made and used in some examples below. Of
course the method demonstrated in the cells that follow can be used on any
expression not only matrices.

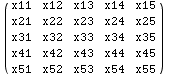
Part has a powerful feature that many users aren't aware of.  The expression
m[[list1,list2]] returns the sub-matrix of (m) formed by the intersection of
the rows given by list1 and the columns given by list2. The next cell gives
an example. This is probably the quickest way to get such a submatrix of (m).

m[[n,list2]] returns a list of elements at positions (list2) in row n. The
next cell gives an example.

Likewise m[[list1,n]] returns a list of elements at positions (list1) of
column n. The next cell gives an example.

Use of the forms demonstrated above gives the fastest way to change  multiple parts of an expression provided the parts can be reached with this  method. Rob Knapp makes this point in a tutorial on Packed Arrays at   http://library.wolfram.com/database/TechNotes/391/.  In that tutorial he shows how this method gives a significant speed  advantage in an implementation of LUDecomposition. This method of changing  multiple values is demonstrated on simple examples in the cells below where  elements of the matrix (m) from above are changed.

Notice the use of All  inside Part is not available in Version 3 or earlier.

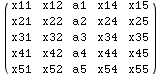
In the next cell All is used to access the first, second and fourth columns
of matrix (m).

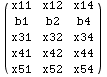
In the next cell we change elements of (m) where rows (1,3) intersect with
columns (2,3,5).

Created by Mathematica  (May 16, 2004)

Back to Ted’s Tricks index page