Partition

Lots of users are not familiar with the Partition function.  Partition is  well documented under Built-in Functions in the Help Browser.  The usage message for this powerful feature is shown below.

A simple demonstration of Partition is given in the next cell.  If the third
argument is not provided the result will be the same as if the a third
argument equal to the second was provided.

The effect of the third argument is demonstrated in the next two examples..

Next we give Partition a fourth argument of 3.  Partition then treats the
list as if it were periodic and ensures the first element of (lst) is the
third element of the first sublist.

Next the fourth argument of Partition is 7 and we get a partition where the
first element of (lst) would be the seventh element of the result if it were
flattened.

Partition can work in higher dimensions. In the next example Partition
seperates a matrix into blocks.

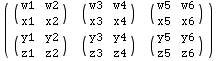
The next example demonstrates that Partition can work on expressions that
don't have the head list.

I haven't been able to find ways to clearly demonstrate use of the Partition
features listed below.  Each of these features are in the Partition usage
message.



•  Partition[list, n, d, {kL, kR}] specifies that the first element
of list should appear at position kL in the first sublist, and the last
element of list should appear at or after position kR in the last sublist.



•  Partition[list, n, d, {kL, kR}, x] pads if necessary by repeating
the element x.



•  Partition[list, n, d, {kL, kR}, {x1, x2, ... }] pads if necessary
by cyclically repeating the elements xi.



•  Partition[list, n, d, {kL, kR}, {}] uses no padding, and so can
yield sublists of different lengths.



•  Partition[list, nlist, dlist, {klistL, klistR}, padlist] specifies
alignments and padding in a nested list.

Created by Mathematica  (May 16, 2004)

Back to Ted’s Tricks index page