Tricks_L-O_21.html

Outer

The first two examples demonstrate the basic use of Outer.

A user asked the MathGroup how to define tables like the one below, but
having larger dimensions without writing the whole table explicitly?

{{f1[x1], f1[x2], f1[x3], f1[x4]}, {f2[x1], f2[x2], f2[x3], f2[x4]}, {f3[x1], f3[x2], f3[x3], f3[x4]}, {f4[x1], f4[x2], f4[x3], f4[x4]}}

Bob Hanlon provided the following solution.

The next cell does the same thing, and is based on an example in the Help
Browser.

The next cell shows what we get for the outer product of two matrices.

( ( f[a11, b11] f[a11, b12] ) ( f[a12, b11] f[a12, b12] ... 0;) f[a21, b21] f[a21, b22] f[a22, b21] f[a22, b22]

The next cell flattens what we get from the computing Outer with 4 lists.

{h[a1, b1, c1, d1], h[a1, b1, c1, d2], h[a1, b1, c2, d1], h[a1, b1, c2, d2], h[a1, b2, c1, d1] ... 1], h[a3, b2, c2, d2], h[a3, b3, c1, d1], h[a3, b3, c1, d2], h[a3, b3, c2, d1], h[a3, b3, c2, d2]}

In the next two examples we provide integers as additional arguments.

( ( f[a11, {b11, b12}] ) ( f[a12, {b11, b12}] ) > ... , b12}] ) f[a21, {b21, b22}] f[a22, {b21, b22}]

( ( f[{a11, a12}, b11] ) ( f[{a11, a12}, b21] ) > ... }, b21] ) f[{a21, a22}, b12] f[{a21, a22}, b22]

Part[expr,0] is always the same as Head[expr], but Head is a bit faster since
it doesn't need to determine what part. For example Part[1+π, 0] returns
Plus.

In the next cell we see the part at position (2,0) of the list {1,1+π} is
Plus.

In the next cell a matrix (m) is made and used in some examples below. Of
course the method demonstrated in the cells that follow can be used on any
expression not only matrices.

Clear["Global`*"] ;  m = {{x11, x12, x13, x14, x15}, {x21, x22, x23, x24, x2 ... 34, x35}, {x41, x42, x43, x44, x45}, {x51, x52, x53, x54, x55}} ;   MatrixForm[m]

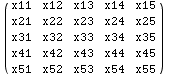
( x11 x12 x13 x14 x15 ) x21 x22 x23 x24 x25 ... 32 x33 x34 x35 x41 x42 x43 x44 x45 x51 x52 x53 x54 x55

Part has a powerful feature that many users aren't aware of. The expression
m[[list1,list2]] returns the sub-matrix of (m) formed by the intersection of
the rows given by list1 and the columns given by list2. The next cell gives
an example. This is probably the quickest way to get such a submatrix of (m).

m[[n,list2]] returns a list of elements at positions (list2) in row n. The
next cell gives an example.

Likewise m[[list1,n]] returns a list of elements at positions (list1) of
column n. The next cell gives an example.

Use of the forms demonstrated above gives the fastest way to change multiple parts of an expression provided the parts can be reached with this method. Rob Knapp makes this point in a tutorial on Packed Arrays at http://library.wolfram.com/database/TechNotes/391/. In that tutorial he shows how this method gives a significant speed advantage in an implementation of LUDecomposition. This method of changing multiple values is demonstrated on simple examples in the cells below where elements of the matrix (m) from above are changed.

Notice the use of All inside Part is not available in Version 3 or earlier.

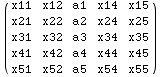
( x11 x12 a1 x14 x15 ) x21 x22 a2 x24 x25 ... 32 a3 x34 x35 x41 x42 a4 x44 x45 x51 x52 a5 x54 x55

( x11 x12 a1 x14 x15 ) b1 b2 b3 b4 b5 ... 32 a3 x34 x35 x41 x42 a4 x44 x45 x51 x52 a5 x54 x55

In the next cell All is used to access the first, second and fourth columns
of matrix (m).

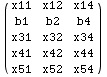
( x11 x12 x14 ) b1 b2 b4 x31 x32 x34 x41 x42 x44 x51 x52 x54

In the next cell we change elements of (m) where rows (1,3) intersect with
columns (2,3,5).

( x11 jjj1 jjj2 x14 jjj3 ) b1 b2 b3 b4 b5 ... x34 kkk3 x41 x42 a4 x44 x45 x51 x52 a5 x54 x55

PatternTest is closely related to Condition. PatternTest is used to specify that a certain pattern must meet a certain condition. So for example in the next cell (f) is defined when given an argument that is a positive number.

$Clear[f, s]  f[x_ ? Positive] := x + 1  {f[2], f[8.3], f[π/2], f[(-2)^(1/2)]}$

${3, 9.3, 1 + π/2, f[ 2^(1/2)]}$

In the next example (f) is only defined when given an argument that is a
positive integer.

$Clear[f, s]  f[x_Integer ? Positive] := x + 1  {f[2], f[8.3], f[π/2], f[(-2)^(1/2)]}$

${3, f[8.3], f[π/2], f[ 2^(1/2)]}$

In the next example (f) is defined when given an argument that is a positive
integer or a positive real number.

$Clear[f, s]  f[x : ((_Integer | _Real) ? Positive)] := x + 1  {f[2], f[8.3], f[π/2], f[(-2)^(1/2)]}$

${3, 9.3, f[π/2], f[ 2^(1/2)]}$

In some cases we want to use a test that isn't a built-in unary operator (Positive, NumericQ, AtomQ, ...). In that case we can use a pure function as in the next example. In the next example (f) is only defined when given an argument that is an integer between 0 and 10.

$Clear[f, s]  f[x_Integer ? (0<#<10&)] := x + 1  {f[2], f[25], f[8.3], f[π/2], f[(-2)^(1/2)]}$

${3, f[25], f[8.3], f[π/2], f[ 2^(1/2)]}$

In the next cell (f) is only defined when given an argument of any type
between 0 and 10. Can you see why we need the part about (Im[#]===0) ?

$Clear[f, s]  f[x_ ? (Im[#] === 0&&0<#<10&)] := x + 1  {f[2], f[25], f[8.3], f[π/2], f[(-2)^(1/2)]}$

${3, f[25], 9.3, 1 + π/2, f[ 2^(1/2)]}$

We can't use pattern variables in the test portion of (Pattn/;Test), and that
is why the definition in the next cell isn't used.

Created by Mathematica (May 16, 2004)