Where definitions are stored
The order that definitions are stored and changing the order of the definitions is discussed in sections 2.4.7 and 2.4.13 of The Mathematica Book.
In some cases you might also need to write a function that will automatically examine the definitions of a certain symbol. Your function might then return part of those definitions or automatically make changes to some of the definitions. In order to do this you need to know where the definitions are stored. Mathematica stores definitions as DownValues, UpValues, OwnValues, NValues, SubValues, FormatValues, DefaultValues, and Messages. Except for ![Attributes[symb]](../HTMLFiles/Tricks_Misc_180.gif) and Options[symb] anything that affects evaluation of expressions involving symb are stored in one of these places and they are each discussed below.
and Options[symb] anything that affects evaluation of expressions involving symb are stored in one of these places and they are each discussed below.
If you evaluate (??symb) all information asssociated with symb is displayed, except the only message displayed is (symb::usage) and only if symb has a usage message.
DownValues
Definitions made using (f[args] := rhs) are stored in DownValues[f] as
demonstrated with the next cell.
![ClearAll[f, x, y] ; x = 4 ; f[x_, y_] := x^2 - y^2 <br /> DownValues[f]](../HTMLFiles/Tricks_Misc_181.gif)
![{HoldPattern[f[x_, y_]] x^2 - y^2}](../HTMLFiles/Tricks_Misc_182.gif)
Definitions made using (f[args] = rhs) are also in DownValues[f] as
demonstrated with the next cell.
![ClearAll[f] ; f[x_, y_] = x^2 - y^2 <br /> DownValues[f]](../HTMLFiles/Tricks_Misc_183.gif)
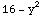
![{HoldPattern[f[x_, y_]] 16 - y^2}](../HTMLFiles/Tricks_Misc_185.gif)
UpValues
Definitions made using (f/: lhs ^:= rhs) are stored in UpValues[f] as
demonstrated with the next cell.
![ClearAll[f] ; x = 4 ; f[x_] + f[-x_]^:=2 f[x] <br /> UpValues[f]](../HTMLFiles/Tricks_Misc_186.gif)
![{HoldPattern[f[-x_] + f[x_]] 2 f[x]}](../HTMLFiles/Tricks_Misc_187.gif)
Definitions made using (f/: lhs := rhs) are also stored in UpValues[f].
![ClearAll[f, g] ; f/:f[x_] + g[y_] := {x, y} ; UpValues[f]](../HTMLFiles/Tricks_Misc_188.gif)
![{HoldPattern[f[x_] + g[y_]] {x, y}}](../HTMLFiles/Tricks_Misc_189.gif)
On rare occasions it's wise to store definitions using (f[args] ^= rhs) and
these definitions are also stored in UpValues[f].
![ClearAll[f, g] ; f[x_] + g[y_]^={x, y} ; <br /> UpValues[f]](../HTMLFiles/Tricks_Misc_190.gif)
![{HoldPattern[f[x_] + g[y_]] {4, y}}](../HTMLFiles/Tricks_Misc_191.gif)
Use of (f/: lhs = rhs) isn't even documented, but it seems to give the
expected result and it also makes a definition stored in UpValues[f].
![ClearAll[f, g] ; f/:f[x_] + g[y_] = {x, y} ; UpValues[f]](../HTMLFiles/Tricks_Misc_192.gif)
![{HoldPattern[f[x_] + g[y_]] {4, y}}](../HTMLFiles/Tricks_Misc_193.gif)
OwnValues
Definitions for (symb=expr) and (symb:=expr) are stored in OwnValues[symb].
The next cell assigns a value to expr.
![ClearAll[expr, x] ; expr = 2 + x ;](../HTMLFiles/Tricks_Misc_194.gif)
Next we see the above definition is stored in OwnValues[expr].
![OwnValues[expr]](../HTMLFiles/Tricks_Misc_195.gif)
![{HoldPattern[expr] 2 + x}](../HTMLFiles/Tricks_Misc_196.gif)
NValues
Definitions for N[f[args]] are stored in NValues[f]. The next cell makes a
definition for N[f[x_,y_]].
![ClearAll[f] ; N[f[x_, y_]] := N[{x, y, 0, 0, 0}]](../HTMLFiles/Tricks_Misc_197.gif)
The above definition isn't used to evaluate the next cell because N wasn't
used.
![f[π, 3^(1/2)]](../HTMLFiles/Tricks_Misc_198.gif)
![f[π, 3^(1/2)]](../HTMLFiles/Tricks_Misc_199.gif)
In the next cell our definition for N[f[x_,y_]] is used.
![N[f[π, 3^(1/2)]]](../HTMLFiles/Tricks_Misc_200.gif)
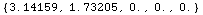
Our definition for N[f[x_,y_]] is stored in NValues[f].
![NValues[f]](../HTMLFiles/Tricks_Misc_202.gif)
![{HoldPattern[N[f[x_, y_]]] N[{x, y, 0, 0, 0}]}](../HTMLFiles/Tricks_Misc_203.gif)
SubValues
Definitions for f[arg1][args] are stored in SubValues[f]. This is
demonstrated with the next cell.
![ClearAll[f, a, x, y] ; f[a_][x_, y_] := {a, x^2 - y^2}](../HTMLFiles/Tricks_Misc_204.gif)
![SubValues[f]](../HTMLFiles/Tricks_Misc_205.gif)
![{HoldPattern[f[a_][x_, y_]] {a, x^2 - y^2}}](../HTMLFiles/Tricks_Misc_206.gif)
![ClearAll[f, Subscript] f_1[x_, y_] := x^2 - y^2 ; f_1[4, 1]](../HTMLFiles/Tricks_Misc_209.gif)
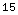
![SubValues[Subscript]](../HTMLFiles/Tricks_Misc_211.gif)
![{HoldPattern[f_1[x_, y_]] x^2 - y^2}](../HTMLFiles/Tricks_Misc_212.gif)
FormatValues
A user once wrote to the MathGroup asking how one could ensure rational numbers greater than one are displayed as improper fractions.  of Wolfram Research gave the solution below to change the way rational numbers are formated.
of Wolfram Research gave the solution below to change the way rational numbers are formated.
![Unprotect[Rational] ; Format[Rational[num_Integer, den_Integer]/;Abs[num/den] >1] := ... den]], FractionBox[ToString[Mod[num, den]], ToString[den]] } ] ]](../HTMLFiles/Tricks_Misc_214.gif)
After evaluating the cell above the output of the next cell is formatted as
an improper fraction.
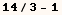
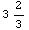
Below we see that the above definition is stored in FormatValues[Rational].
![FormatValues[Rational]](../HTMLFiles/Tricks_Misc_217.gif)
![{HoldPattern[MakeBoxes[Rational[num_Integer, den_Integer]/;Abs[num/den] >1, FormatType_]] & ... ]/;Abs[num/den] >1] ToString[Quotient[num, den]] ToString[Mod[num, den]]/ToString[den]}](../HTMLFiles/Tricks_Misc_218.gif)
Before you continue you might want to evaluate the next cell to restore the
default formatting of rational numbers.
![FormatValues[Rational] = {} ; Protect[Rational] ;](../HTMLFiles/Tricks_Misc_219.gif)
MakeBoxes is similar to Format and FormatValues, and definitions using MakeBoxes are stored in ![DownValues[MakeBoxes]](../HTMLFiles/Tricks_Misc_220.gif) or possibly in UpValues for the type of expression being formatted.
or possibly in UpValues for the type of expression being formatted.
DefaultValues
Anything stored using Default[f], Default[f,i], or Default[f,i,n] is stored in DefaultValues[f]. The built-in functions Plus, Times and Power have defaults stored as DefaultValues as the next cell shows. Use of Default was explained in an earlier section.
![DefaultValues[Plus] DefaultValues[Times] DefaultValues[Power]](../HTMLFiles/Tricks_Misc_221.gif)
![{HoldPattern[Default[Plus]] 0}](../HTMLFiles/Tricks_Misc_222.gif)
![{HoldPattern[Default[Times]] 1}](../HTMLFiles/Tricks_Misc_223.gif)
![{HoldPattern[Default[Power, 2]] 1}](../HTMLFiles/Tricks_Misc_224.gif)
Options are also stored in DefaultValues as demonstrated with the next cell.
![DefaultValues[Cancel]](../HTMLFiles/Tricks_Misc_225.gif)
![{HoldPattern[Options[Cancel]] {ExtensionNone, Modulus0, TrigFalse}}](../HTMLFiles/Tricks_Misc_226.gif)
You could use DefaultValues to see what options a function has or change the options, but I can't see why anyone would want to do this. Since options are stored as DefaultValues you should be cautious about using ![DefaultValues[symb] = {}](../HTMLFiles/Tricks_Misc_227.gif) to delete all defaults.
to delete all defaults.
In the next cell I assign a value to Default[f1,2] and I give f1 options.
![ClearAll[f1] ; Default[f1, 2] = {1} ; Options[f1] = {opt1val1, opt3val3} ;](../HTMLFiles/Tricks_Misc_228.gif)
The next cell shows that the previous definitions are stored in
DefaultValues[f1].
![DefaultValues[f1]](../HTMLFiles/Tricks_Misc_229.gif)
![{HoldPattern[Default[f1, 2]] {1}, HoldPattern[Options[f1]] {opt1val1, opt3val3}}](../HTMLFiles/Tricks_Misc_230.gif)
Messages
The next cell makes Messages related to the symbol foo.

At times you might want to check on or manipulate the messages above. The
next cell gives us the list of messages as they are stored.
![Messages[foo]](../HTMLFiles/Tricks_Misc_232.gif)
![{HoldPattern[foo :: err1] foo had invalid input., HoldPattern[foo :: err2] foo got stuck., HoldPattern[foo :: usage] foo is a Symbol.}](../HTMLFiles/Tricks_Misc_233.gif)
Below we see that evaluating (??foo) displays the usage message for foo, but
not the error messages for foo.
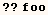
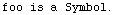
Created by
Mathematica
(May 17, 2004)
![ClearAll[f, x, y] ; x = 4 ; f[x_, y_] := x^2 - y^2 <br /> DownValues[f]](../HTMLFiles/Tricks_Misc_181.gif)
![ClearAll[f] ; x = 4 ; f[x_] + f[-x_]^:=2 f[x] <br /> UpValues[f]](../HTMLFiles/Tricks_Misc_186.gif)
![Unprotect[Rational] ; Format[Rational[num_Integer, den_Integer]/;Abs[num/den] >1] := ... den]], FractionBox[ToString[Mod[num, den]], ToString[den]] } ] ]](../HTMLFiles/Tricks_Misc_214.gif)
![{HoldPattern[MakeBoxes[Rational[num_Integer, den_Integer]/;Abs[num/den] >1, FormatType_]] & ... ]/;Abs[num/den] >1] ToString[Quotient[num, den]] ToString[Mod[num, den]]/ToString[den]}](../HTMLFiles/Tricks_Misc_218.gif)