RotateRight, RotateLeft

RotateRight and RotateLeft can be used on an expression that doesn't have the
head List.  In the two cells below the arguments of an expression are rotated
two places to the right and two places to the left.

Normally RotateRight and RotateLeft are used on a simple list and the second
argument (if present) is normally an integer.  However, the second argument
can be a list of integers.  First consider the tensor (m2) below.

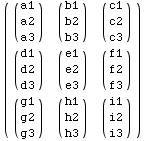
First the default case for RotateRight is demonstrated on the above tensor.

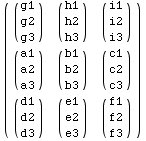
In the cell below we see the default case is equivalent to a few values for
the second argument.

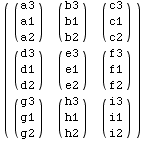
When the second argument is {0,1} or {0,1,0} the second level is rotated one
place.

When the second argument is {0,0,1} the third level is rotated one place.

Created by Mathematica  (May 16, 2004)

Back to Ted’s Tricks index page